Programming

Share this step
Before quantum computers existed, quantum algorithms were defined either mathematically, in terms of the transitions on quantum states, or using a graphical circuit notation for individual gates. Nowadays, quantum computers can be programmed using a GUI for the graphical notation, an assembly language-like text notation for the equivalent gates, or richer programming languages that may also provide low-level access.
The effects of the gates described earlier are similar to the logic gates we use to build a classical computer, like AND and OR. These days, few people bother designing their own programs for classical computers using those low-level gates. In fact, due to the fixed structure of a classical computer, it is hard to select which gates are used. Instead, we program computers using programming languages that humans can read, which are then turned into instructions for the computer, like ADD or MULTIPLY.
When we construct quantum algorithms, we will use gates. Each gate will operate on one, two or three qubits, and we will apply a sequence of gates to our register to form a complete circuit, an implementation of an algorithm. In most quantum computer implementations, the qubits are stationary, and gates are executed on the qubits where they sit, allowing us to treat them something like low-level computer instructions.
Graphical Notation
Each of the gates discussed back in Step 2.15 has a symbol, shown in the figure at the top of this article. Circuits are composed to run left to right, with a horizontal line for each qubit. The visual resemblance to music has lead IBM to referring to such a diagram as a “score”. IBM’s web-based interface uses drag-and-drop programming with colorful, stylized gate symbols.
This approach can show conditional operation, basing the choice to execute individual gates on the outcome of prior measurements. It is also common to draw circuits in terms of blocks of primitive gates. However, it is inherently difficult to create a loop or complex control structures.
A Simple “Assembly” Language
During my (Van Meter’s) Ph.D. thesis work, I developed a simple “assembly” language that lists gates by name, and the qubits on which they operate by a variable name, rather than a physical location. Other low-level languages might make similar choices, or might more directly specify the unitary transform and might identify qubits by physical location, but the goal and program structure will be similar. One unique feature of my language is that the programmer explicitly specifies which gates may be executed at the same time, denoted by the numeric labels. Other assembly languages depend on the compilation tools to determine this parallelism.
1: CCNOT A0 B0 C0
CCNOT A1 B1 C1
CCNOT A2 B2 C2
2: CNOT A1 B1
CNOT A2 B2
CNOT A3 B3
3: CCNOT C0 B1 C1
4: CCNOT C1 B2 C2
One modern tool is OpenQASM,
developed by Andrew Cross and others at IBM.
Programming Languages
The notion of quantum programming languages goes back to the earliest
days of quantum computing research, but much of the early work was
very abstract. Omer’s QCL was one of the first concrete, publicly
available languages, and also provided a simple simulator.
Several years ago, the IARPA Quantum Computer Science program resulted
in the development of several languages.
Quipper (by a team from Dalhousie
University, U. Penn, and IAS in Princeton) builds on the Haskell
programming language.
Scaffold
(from a team including Princeton University) is a C-like language.
QuaFL (from BBN)
is a from-scratch functional language.
Microsoft is now on their second-generation language, known as Q#
(Q-sharp).
More recently, efforts have turned toward simple library extensions
for the popular programming language Python.
QISKit and OpenQASM, for connecting to the
IBM machines, looks like this:
# quantum circuit to make an entangled bell state
bell = Q_program.create_circuit('bell', [qr], [cr])
# H (Hadamard) gate to qubit 0 in the Quantum Register "qr"
bell.h(qr[0])
# CNOT (Controlled-NOT) gate from qubit 0 to qubit 1
bell.cx(qr[0], qr[1])
Rigetti, a startup company making superconducting quantum computers,
has developed PyQuil and
the Forest programming environment.
Common Subroutines
Of course, quantum algorithms depend on a number of common building
blocks, or subroutines. (Just to confuse things, quantum
researchers occasionally call an entire block of gates a “gate”,
also.) Some of these build on classical notions of simple circuits
such as adders, or are quantum-specific routines such as the quantum
Fourier transform (QFT).
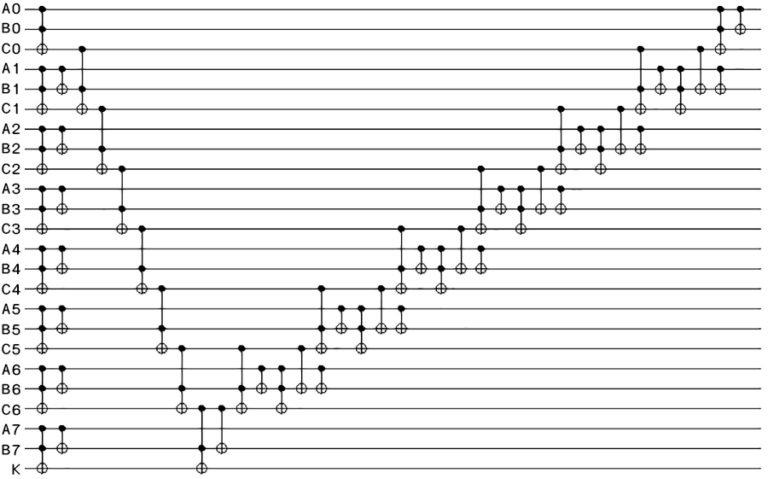
The image below is a circuit for adding two eight-qubit registers
together. This design, by Vedral, Barenco and Ekert, is based on a
classical form of circuit known as a ripple-carry adder, a binary
form of the right-to-left method you learned as a child. Extra qubits
are used to hold partial, temporary results. The “V” shape comes from
the need to disentangle those temporary qubits from the important data
qubits, and the severe restriction that the entire block must be
unitary, or reversible.
We can expect that such low-level routines will be provided as
libraries of functions in programming toolkits, allowing us to compose
our own algorithms at a high level of abstraction.
プログラミング
量子コンピュータが作られる以前、量子アルゴリズムはどれも、量子状態の遷移を表現した数学的な定義付けか、個々のゲートを記述していく回路表記法を利用した定義付けがなされていました。 現在、量子コンピュータは、視覚的な回路表記を用いたGUI(グラフィカルユーザインターフェース)、ゲートのためのアセンブリ言語のようなテキスト表記、低レベルのアクセスを提供しているより高級プログラミング言語のいずれかを用いることでプログラミングができます。
前に説明したゲートの効果は、ANDやORのような古典的なコンピュータの構築に用いられる論理ゲートのそれと似ています。 現在は、このような単純なゲートを使って古典コンピュータのプログラムを設計する人は殆どいません。 実際、現代のコンピュータの構造は非常に複雑にできているため、どのゲートを使用すべきかを考えることは簡単なことではありません。 多くの場合は、人間が読むことのできるプログラミング言語を使ってプログラムを記述し、その後、そのプログラムをADDやMULTIPLY等のコンピュータが理解できる命令に変換しています。
量子アルゴリズムはゲートを用いて構築されます。 各ゲートは1つ、2つまたは3つの量子ビットで実行され、一連のゲートをレジスタに適用してアルゴリズムの実装として完全な回路を形成します。 殆どの量子コンピュータの実装では、量子ビットは物理的に静的であり、ゲート操作はそこに存在する適切な量子ビットに直接実行されるため、ゲートは、低レベルのコンピュータ命令のように扱うことができます。
視覚的表記法
このページの冒頭にある画像のように、2.15 で述べた各ゲートには対応した専用の記号が存在しています。 回路は各量子ビットから水平に伸びる線上に描かれ、左から右へ順番に計算されていきます。 楽譜と視覚的に似ていることから、IBMはこのような回路図を「スコア」と呼んでいます。 IBMのWebベース・インターフェースでは、カラフルでスタイリッシュなゲートのシンボルによるドラッグ・アンド・ドロップ・プログラミングが可能です。
この方法を使って、先に行った測定の結果に基づいたゲートの実行、いわゆる条件付き操作を表すこともできます。 基本的なゲートの集合を単位とした回路を描くことも一般的です。 しかし、ループや複雑な制御構造を表現することは本質的に困難です。
単純なアセンブリ言語
私(バンミーター)の博士論文の中で、私はゲートをその名前で列挙し、ゲートが実行される量子ビットを物理的な位置でなく変数名で指定していくシンプルな “アセンブリ”言語を開発しました。 他の低レベル言語も同様の選択肢を採用するかもしれませんし、ユニタリー変換をより直接的に指定したり、物理的な位置によって量子ビットを指定したりするものもあるかもしれませんが、目標とプログラム構造はある程度の類似性がのこるはずです。 私の言語のユニークな特徴の1つは、同時に実行すべきゲートをプログラマが数値のラベルを付けることで明示的に指定できることです。 他のアセンブリ言語では、この並列性はコンパイルツールの判断に委ねられています。
1: CCNOT A0 B0 C0
CCNOT A1 B1 C1
CCNOT A2 B2 C2
2: CNOT A1 B1
CNOT A2 B2
CNOT A3 B3
3: CCNOT C0 B1 C1
4: CCNOT C1 B2 C2
現在用いられている言語の一例として、IBMのAndrew Cross等によって開発されたOpenQASMが挙げられます。
プログラミング言語
量子プログラミング言語の概念は、量子計算の研究の初期に遡りますが、その頃の研究の多くは非常に抽象的でした。 OmerのQCLは最初に公開された完成した言語の1つであり、シンプルなシミュレータも提供していました。
数年前、IARPA Quantum Computer Scienceプログラムは、その成果としていくつかの言語を開発しました。 Quipper(カナダ・ダルハウジー大学、米国ペンシルベニア大学、米国プリンストン大学の IASのチームによる)は、Haskellプログラミング言語で構築されています。 Scaffold(プリンストン大学を含むチームによる)はC言語のような言語です。 QuaFL(BBN Tehnologies 社による)は、ゼロから開発した関数型言語です。
最近では、MicrosoftがQ#(キューシャープ)という、彼らにとっては第二世代となるプログラミング言語を利用しています。
また、ポピュラーなプログラミング言語であるPythonでつかえる簡単なライブラリの拡張にも力が入っています。例えば、 QISKitとOpenQASMは、IBMマシンに接続するためのPython ライブラリで、具体的には以下のような記述が可能です。
# quantum circuit to make an entangled bell state
bell = Q_program.create_circuit('bell', [qr], [cr])
# H (Hadamard) gate to qubit 0 in the Quantum Register "qr"
bell.h(qr[0])
# CNOT (Controlled-NOT) gate from qubit 0 to qubit 1
bell.cx(qr[0], qr[1])
超電導量子コンピュータを作っているRigettiというスタートアップの会社は、Pythonライブラリである PyQuil と プログラミング環境である Forest を開発しました。
共通サブルーチン
もちろん、量子アルゴリズムは、共通に利用可能な構成要素(あるいはサブルーチン)を積極的に活用してします。 (混乱を招きますが、量子計算の研究者は、ゲートの組み合わせ(構成要素)全体を「ゲート」と呼ぶこともあります。) これらの中には、加算器などの単純な回路の古典的概念に基づくものもあれば、量子フーリエ変換 (QFT)のような量子特有のものもあります。
下の画像は、2つの8量子ビットレジスタを加算するための回路です。 Vedral、Barenco、Ekertによるこの設計は、右から左への方法のバイナリ形式のリップルキャリー加算器として知られている古典的な回路に基づいています。 一時的な結果を保持するために余分に1量子ビットを使用します。 “V”字形は、重要なデータ量子ビットから一時的な量子ビットを解放する必要と、量子回路がユニタリー、または可逆でなければならないという厳しい制限から来ています。

このような低レベルのルーチンがプログラミングツールキットの関数ライブラリとして提供されるようになれば、我々は、高い抽象度で独自のアルゴリズムを作成することに注力できるようになります。
Share this

Reach your personal and professional goals
Unlock access to hundreds of expert online courses and degrees from top universities and educators to gain accredited qualifications and professional CV-building certificates.
Join over 18 million learners to launch, switch or build upon your career, all at your own pace, across a wide range of topic areas.
Register to receive updates
-
Create an account to receive our newsletter, course recommendations and promotions.
Register for free








