How to Label Flexagons

We can label flexagons using Les Pook’s flexagon symbols. These symbols are great because they identify flexagons at a glance and contain important information about their structure and dynamics. We need one more ingredient though before we get to the flexagon symbol – the Schläfli symbol.

The Schläfli symbol

Ludwig Schläfli was a 19th century Swiss mathematician who specialised in geometry, especially known for his influential work on geometry in high dimensions. Schläfli developed a symbol, the Schläfli symbol, for polygons, polyhedra and polytopes in higher dimensions.

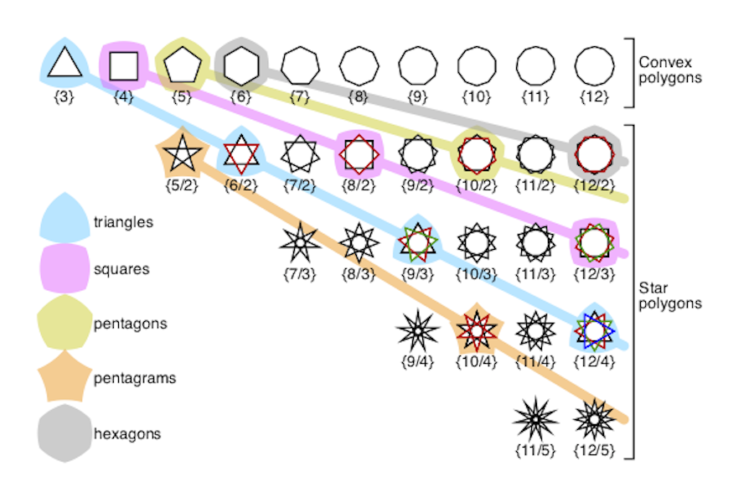
You can see the Schläfli symbols for some regular polygons in the image above. The Schläfli symbol for a regular polygon is just the number of vertices (or edges) written inside curly brackets: {3} for an (equilateral) triangle, {4} for a square, {5} for a regular pentagon, {6} for a regular hexagon, etc. The Schläfli symbol for a star polygon (a non-convex regular polygon) is a fraction written inside curly brackets. The numerator is the number of vertices and the denominator is the number of vertices skipped when drawing each edge of the star, plus 1. For example, when drawing a line from point to point on the pentagram (5-pointed star) we skip over 1 point of the star, so its Schläfli symbol is {5/2} (remember to add 1 to the denominator). The Schläfli symbol for a nonagram (9-pointed star) is {9/3} because 3 points are skipped.

Flexagon symbols

Pook created a flexagon symbol that uses the Schläfli symbol. Pook’s flexagon symbol (usually) has 3 components. The first is the number of sectors the flexagon has. The second is the Schläfli symbol of the constituent polygon of the flexagon. For example, the constituent polygon of both the tri-hexa- and the hexa-hexa-flexagons is a triangle. It’s Schläfli symbol is {3}, so 3 is the second component of the flexagon symbol for both these flexagons.

The third component is what’s called the flexagon net symbol. It is the Schläfli symbol of a polygon that describes the dynamics of the flexagon – corresponding to the flexagon’s state diagram and flexes between states. This polygon is known as the associated polygon, not to be confused with the constituent polygon – the basic shape of the individual leaves. Here is how to find all the possible associated polygons of a given constituent polygon:

• Draw the constituent polygon (i.e. triangle for flexagons made from triangles, square for flexagons made from squares etc.)
• Choose any edge as a starting point, and draw a straight line between its center and the center of the edge adjacent to it.
• Do this until you return to the edge where you started
• The shape formed – the inscribed polygon – is the trivial associated polygon for this constituent shape and is the same shape as the constituent polygon (i.e. you’ll get a triangle for a triangle, square for a square etc.)
• For pentagons, heptagons and higher, repeat the process, but this time draw the lines between every other edge. If all edges are connected, this inscribed polygon is another associated polygon (it will be a star polygon).
• If possible, repeat the process, but this time draw the lines between every third edge. If all edges are connected, this is another associated polygon.
• Continue until no further “skips” are available.

In the image above, the polygons that are unicolored black are all the possible associated polygons corresponding to the regular polygons up to 12. Those that have two or more colors (i.e. {6/2}, {8/2}…) are not “ associated polygons.

Creating flexagon templates once you know the associated polygons is easy.

To create a template for a first order fundamental flexagon, you need to:

• Choose the number of sectors you want (must be two or more). The number of leaves in each sector must equal the number of edges of the constituent polygon.
• For each sector draw the constituent polygons in a zigzag strip, connecting polygons so that the shortest distance between every two hinges is equal to the denominator of the Schläfli symbol for the associate polygon minus 1, i.e. a (shortest) distance of no edges for whole number Schläfli symbols, 1 edge for those whose Schläfli symbol denominator is 2 etc., and making sure the hinge angles is the same and the sign of the hinge angle alternates. In the following image you can see two examples of such nets.

For second order fundamental templates the same routine is performed, except that this time the template will be “wavy” because you need to make sure that the signs on pairs of hinge angles alternate.

Interestingly, if you inscribe the associated polygon within its corresponding constituent polygon, you get a flexagon diagram or map resembling Tuckerman diagrams – i.e. they describe the main flex cycles between states.

• The edges of the circumscribing polygon are the main states of the flexagon
• The vertices of the circumscribing polygon are the intermediate states of the flexagon (i.e. the propeller looking state when you pinch flex a tri-hexa-flexagon). +The edges of the inscribed polygon, the associated polygon, show the flex connections between the states.

Now that we know the language, we can put the pieces together and construct the flexagon symbol. It looks like this (the Schläfli squiggly brackets are omitted):

component 1<component 2, component 3>

i.e.:

Number of sectors<Schläfli symbol of the constituent polygon, Schläfli symbol of the associated polygon>

For the tri-hexa-flexagon the flexagon symbol is: 3<3,3> The magic square flexagon symbol is: 2<4,4>

Sector symbols

Pook went one step further. He also wrote a notation for the sector of a flexagon. The notation starts off the same way as the flexagon symbol, except that the first component, the number of sectors is omitted. Two additional numbers are added to the component 2 and component 3 numbers. These are the number of leaves in each pat of the sector from the highest to the lowest. Note that for some flexagons, the sector symbol is dependent on the state of the flexagons because the sectors in different states can have a different number of leaves in each pat. The sector symbol for the tri-hexa-flexagon is <3,3,2,1>