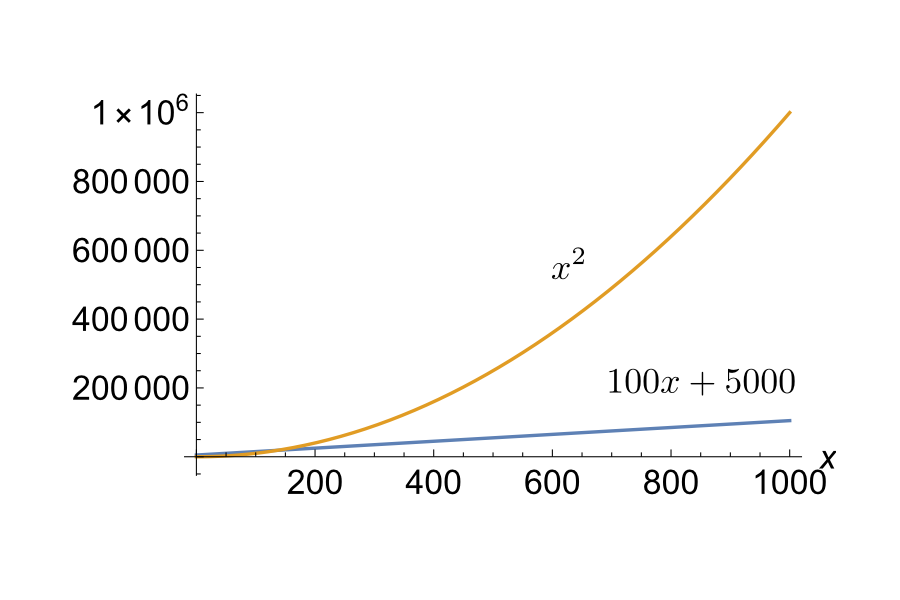
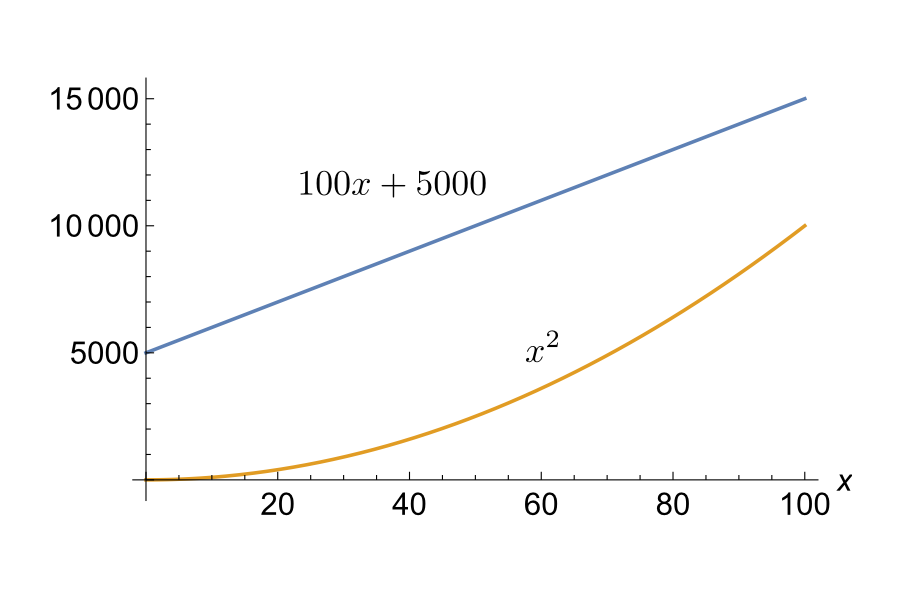
Home / IT & Computer Science / Cloud Computing / 量子コンピュータ入門 / Caveat: Function Growth/注意するポイント:関数の増え方

Reach your personal and professional goals
Unlock access to hundreds of expert online courses and degrees from top universities and educators to gain accredited qualifications and professional CV-building certificates.
Join over 18 million learners to launch, switch or build upon your career, all at your own pace, across a wide range of topic areas.