Market Equilibrium and Price Controls

Share this step
In this article, Dr Matthias Dahm takes a closer look at market equilibrium and price controls.
We start by considering a market without price controls. Figure 1 represents a competitive market. The aim of the graphical representation is to explore market exchanges. The horizontal axis indicates the quantity and the vertical axis the price of the good. Figure 1 shows a demand function, which represents consumers in the market. It indicates for each price a quantity demanded. The demand function can be interpreted as the willingness to pay of consumers for the good. The demand function is downward sloping, because of the law of demand: All other factors being equal, as the price of a good increases, the quantity demanded decreases. In other words, the smaller the quantity demanded, the more the willingness to pay for an additional unit of the good. Figure 1 illustrates this, as at QL the willingness to pay is PH, which is higher than PC at QC.
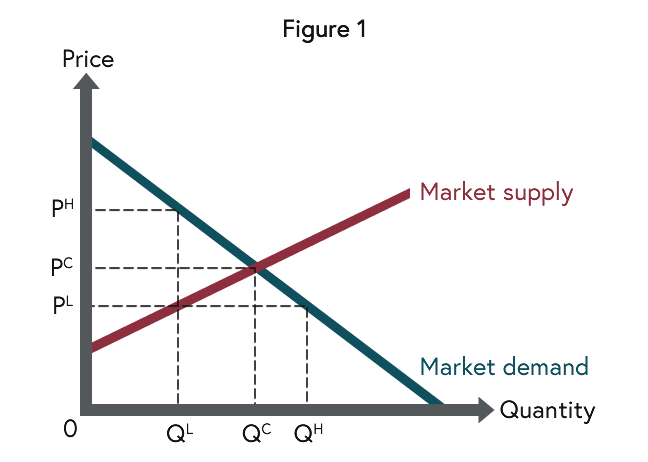 Figure 1
Figure 1
We turn now to the supply side of a market, which represents producers. The supply function indicates for each price a quantity supplied. It can be interpreted as the lowest price that is sufficient for producers to be willing to offer an additional unit in the market. The supply function is upward sloping, because of the law of supply: All other factors being equal, as the price of a good increases, the quantity supplied increases. Again Figure 1 illustrates this, as at QL the minimal price is PL, which is lower than PC at QC.
Once a market has been described using the tools of demand and supply, the next task is to predict the outcome of the market interaction between consumers and producers. Economists think of prices as balancing supply and demand. Markets tend to equilibrium, because prices adjust when for a given price the quantity supplied and the quantity demanded are not compatible. From Figure 1 we see that at the price PC the quantity supplied equals the quantity demanded. In other words, the market is in equilibrium and the quantity QC is exchanged at the price PC. At other prices supply and demand are not compatible. For instance, at the price PL the quantity demanded QH exceeds the quantity supplied QL and so the price tends to rise until PC is reached.
How should we think of a market equilibrium? Economists think that a market equilibrium is efficient. One way to see why this is the case is to consider a smaller quantity than QC, say QL. At that quantity the demand function is higher than the supply function, as PH is larger than PL. This indicates that the consumers’ willingness to pay for the good exceeds the lowest price necessary for producers to be willing to offer an additional unit in the market. Therefore, from society’s point of view, an additional unit should be exchanged. This argument can be repeated until the quantity QC is reached and willingness to pay and minimum price coincide.
Notice that Adam Smith’s metaphor of the ‘invisible hand’ that we encountered in a previous part of the course refers exactly to this property of markets. Even though market participants are not guided by what is best for society, markets lead to efficient situations. This is so, because self-interest leads to a situation in which resources are dedicated to the activities that are most valued, as if guided by an ‘invisible hand’.
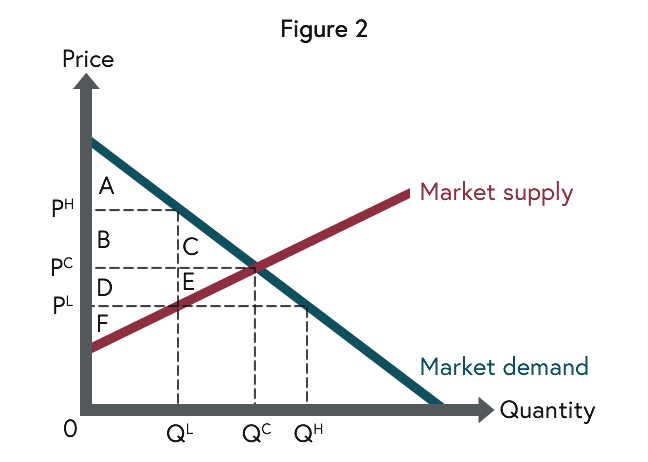 Figure 2
Figure 2
Another way to see that the market equilibrium is efficient builds on the concepts of consumer surplus and producer surplus. Both are a measure of welfare of a given market situation. Consumer surplus builds on the demand function, which again is interpreted as indicating the maximal price consumers are willing to pay for the good. So, as we move along the demand curve (from the left to the right) this maximal price decreases until we reach the market price PC. Thus the area A+B+C represents the value of the good minus the price paid for it, aggregated over the total quantity demanded. This is the consumer surplus generated by the competitive equilibrium. Similarly, producer surplus is measured using the supply function, which is interpreted as indicating the minimal price producers need to produce the good. With this interpretation, the area D+E+F represents the price received minus the production costs of the good, aggregated over the total quantity supplied. This is the producer surplus generated by the competitive equilibrium. The competitive equilibrium is efficient, because it maximises welfare as measured by the sum of consumer and producer surplus. In other words, the area between the demand function and the supply function is maximal: A+B+C+D+E+F. With a smaller quantity than QC this area is reduced, as consumer surplus and producer surplus both reduce to a pentagon. With a larger quantity than QC this area is also reduced, as a “negative area” is added to A+B+C+D+E+F.
We can now use Figure 2 to understand the effects of price controls. We will focus on price controls that rule out the competitive price PC. Suppose that the price cannot exceed PL. Since higher prices are illegal, PL is a maximum price. We have already seen that in a market the price tends to rise towards the equilibrium price PC. But now the new price cannot exceed PL and will hence be exactly PL. At that price the quantity supplied is QL, while the quantity demanded is QH. Since QL is smaller than QH, only QL units will be exchanged. Consequently, consumer surplus is A+B+D, while producer surplus is F. This situation is less efficient than the competitive equilibrium, as the area C+E is lost. It is important to notice that this loss represents consumers who cannot buy the good and producers who are not allowed to profitably participate in the market. There is also a distributive effect. Producers are unambiguously worse-off, as the area F is smaller than the area D+E+F. Consumers lose C and gain D, indicating that those consumers who are successful in buying the good benefit from the low price. But as already pointed out, other consumers are not able to buy the good and are also worse-off.
The preceding is the basic logic for why economists tend to argue that price controls are undesirable and the starting point for a deeper analysis of, for example, the long term effects of such an intervention on demand and supply or the emergence of black markets.
The analysis that Matthias has presented in this article is the analysis that many economists use to argue against price controls. However, price controls still exist at some times and in some places around the world. Comment below why this might be the case.
Share this
The Politics of Economics and the Economics of Politicians

The Politics of Economics and the Economics of Politicians


Reach your personal and professional goals
Unlock access to hundreds of expert online courses and degrees from top universities and educators to gain accredited qualifications and professional CV-building certificates.
Join over 18 million learners to launch, switch or build upon your career, all at your own pace, across a wide range of topic areas.
Register to receive updates
-
Create an account to receive our newsletter, course recommendations and promotions.
Register for free







